一元线性回归的java实现
我们有两组数据,比如连续5年的pv与uv。
我们想预测一下,uv达到500k那么pv会是多少。当然更有意思可能是,如果销售额是500w的话,pv会是多少。
机器学习里的一元线性回归方法是比较简单的方法,就是我们猜是满足y=wx+b的。
那么,按求均方误差的偏导后,可得到如下两公式:
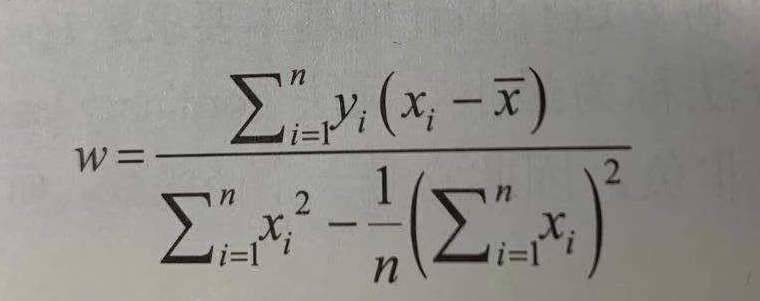
《机器学习》 周志华著 清华大学出版社
下面是求b的公式,要用到w:
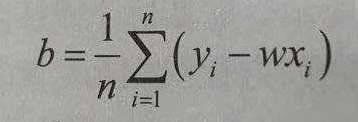
用java代码来实现一下这两公式:
package net.highersoft.svm;
import java.text.DecimalFormat;
import java.util.Arrays;
import java.util.List;
public class TestLineXY {
public static void main(String[] args) {
DecimalFormat df=new DecimalFormat("0.##");
//x pv
//y uv
List<Integer> x=Arrays.asList(5,9,15,19,19,45);
List<Integer> y=Arrays.asList(4,6,12,15,15,37);
/*
List<Integer> x=Arrays.asList(4,6,8,10,12);
List<Double> y=Arrays.asList(7.8d,9.3d,9.9d,11.2d,11.9d);
*/
System.out.println(x+""+y);
if(x.size()!=y.size()) {
System.out.println("分子分母数量不一致。");
return;
}
long sum=0;
for(Integer xi:x) {
sum+=xi;
}
double avgx=sum*1.0/y.size();
System.out.println("avg_x:"+avgx);
//w的分子
double w_molecule=0;
for(int i=0;i<y.size();i++) {
w_molecule+=y.get(i)*(x.get(i)-avgx);
//System.out.print(y.get(i)+"*("+x.get(i)+"-"+avgx+") +");
}
System.out.println();
//System.out.println("w_molecule:"+w_molecule);
//w的分母
double w_denominator=0;
int w_denominator_xi=0;
for(int i=0;i<x.size();i++) {
w_denominator+=Math.pow(x.get(i),2);
w_denominator_xi+=x.get(i);
}
w_denominator=w_denominator-(1.0/x.size())*(Math.pow(w_denominator_xi,2));
//System.out.println("w_denominator:"+w_denominator+" w_denominator_xi:"+w_denominator_xi);
double w=w_molecule/w_denominator;
System.out.println("w:"+w);
double b=1.0/x.size();
double sum_y_wx=0;
for(int i=0;i<x.size();i++) {
sum_y_wx+=(y.get(i)-w*x.get(i));
}
b=b*sum_y_wx;
System.out.println("b:"+b);
String symbol="+";
if(b<0) {
symbol="";
}
System.out.println("y="+df.format(w)+"x"+symbol+df.format(b));
System.out.println(w*15+b);
}
}
相关阅读
评论:
↓ 广告开始-头部带绿为生活 ↓
↑ 广告结束-尾部支持多点击 ↑
